Oreille interne, partie 2 : cellules ciliées et nerf auditif

Dans la précédente section de ce chapitre, nous avons vu comment les vibrations transmises à l’oreille interne excitent localement la membrane basilaire, permettant la décomposition du son en différentes fréquences. Nous allons à présent nous intéresser à la seconde fonction essentielle de l’oreille interne : la conversion des vibrations mécaniques en impulsions électriques. Cette étape, appelée transduction, est fondamentale puisque le cerveau est en mesure de recevoir et traiter des signaux électriques, mais non des vibrations mécaniques.

Nous aborderons ensuite la troisième fonction de la cochlée : l’amplification/compression de l’intensité.

Fig. 68 Schéma du système auditif périphérique mettant en évidence l’oreille interne. (Source : Ivy Livingstone, Biodidac)

Cellules ciliées internes et codage temporel

La conversion de l’onde en courant électrique est assurée par environ 3500 cellules ciliées internes, réparties sur toute la longueur de la membrane basilaire (voir Fig. 69). Comme leur nom l’indique, ces cellules sont dotées, à leur extrémité supérieure, de fins prolongements appelés stéréocils, organisés en rangées de hauteurs croissantes. Ces derniers sont extrêmement sensibles aux mouvements : un déplacement latéral des stéréocils provoque une cascade de réactions électrochimiques qui conduit à une variation du potentiel électrique de la cellule puis à la libération d’un neurotransmetteur, le glutamate. Ce dernier va ensuite se fixer aux récepteurs des fibres du nerf auditif, connectées à la base de la cellule, déclenchant la génération d’un potentiel d’action, une impulsion électrique envoyée aux étages supérieurs du système auditif.

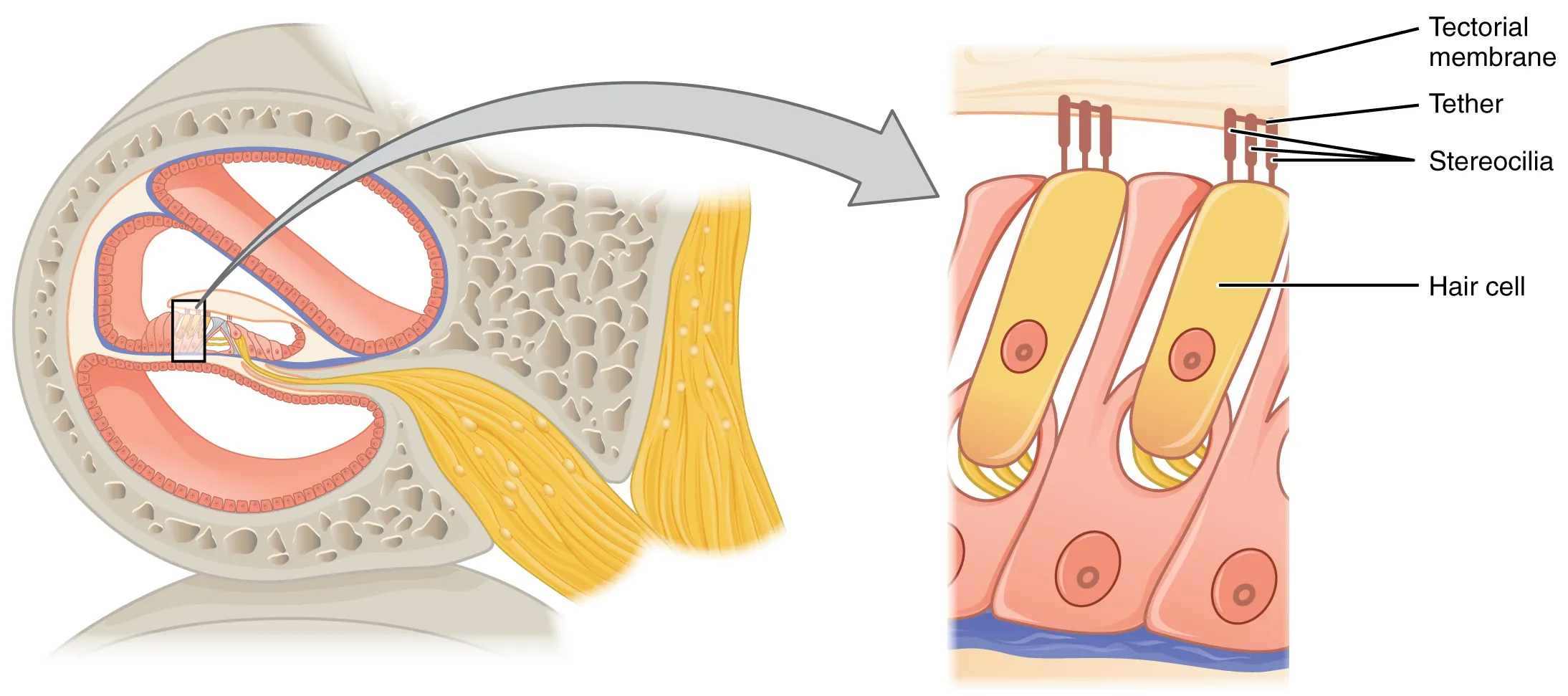
Fig. 69 Schéma de la cochlée en coupe avec un zoom sur les cellules cilliées. (Source : Openstax)

Ainsi, la cellule ciliée est capable de convertir un mouvement latéral de ses stéréocils en une impulsion électrique, ensuite transmise au cerveau. Mais comment cette propriété est-elle exploitée pour coder les vibrations de la membrane basilaire ? La réponse réside dans une structure spécialisée : l’organe de Corti (voir Fig. 70 et Fig. 71). Les cellules ciliées internes décrites plus haut sont attachées à la membrane basilaire, mais leurs stéréocils sont reliés à une seconde membrane, la membrane tectoriale, disposée parallèlement à la première. Lorsqu’une onde sonore progresse le long de la cochlée, elle induit un déplacement vertical de la membrane basilaire. Ce mouvement provoque un glissement des deux membranes l’une par rapport à l’autre, entraînant un déplacement latéral des stéréocils ce qui génère un potentiel d’action dans les fibres du nerf auditif reliées à la cellule.

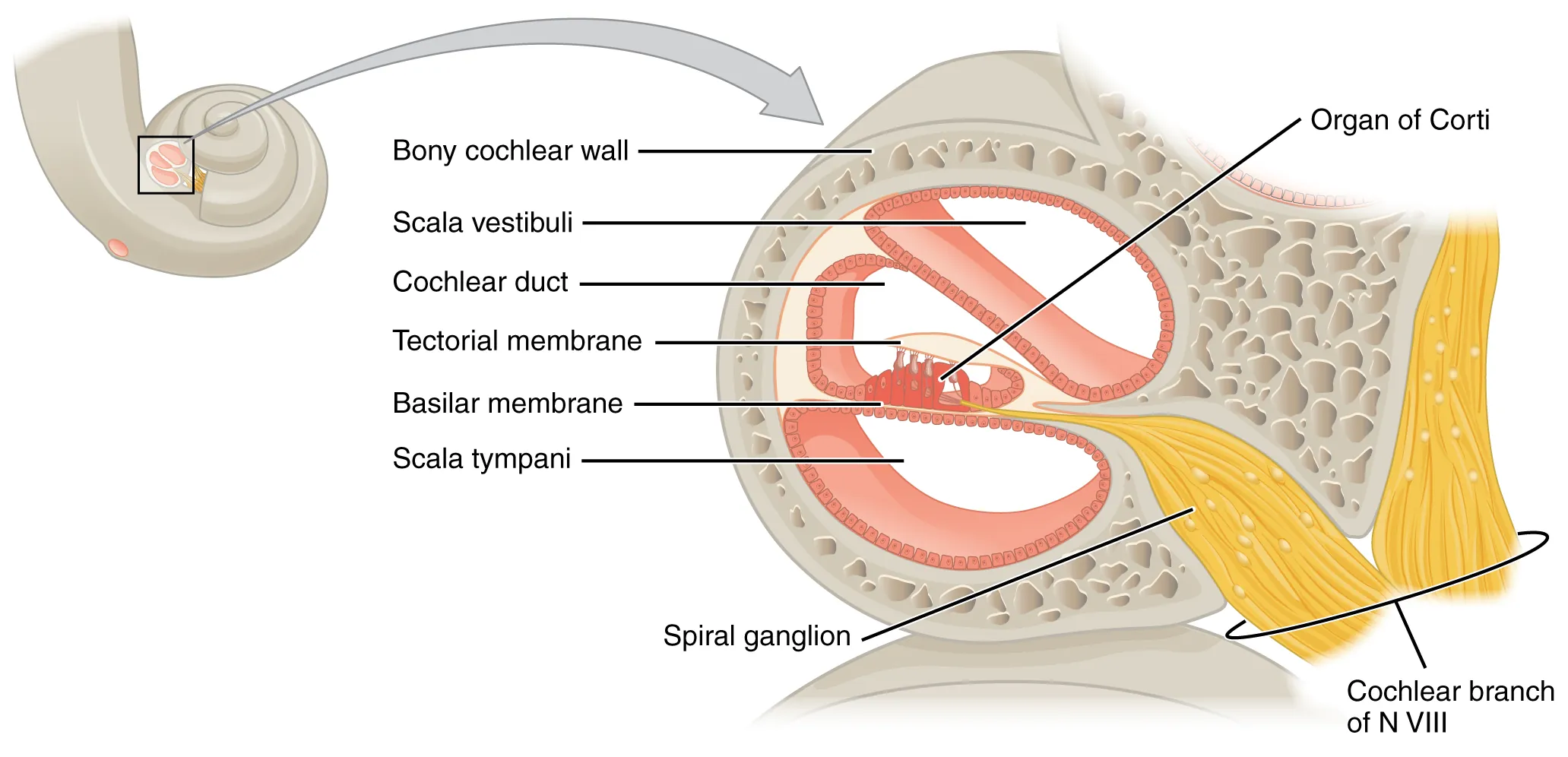
Fig. 70 Schéma de la cochlée en coupe avec un zoom sur l’organe de Corti. (Source : Openstax)

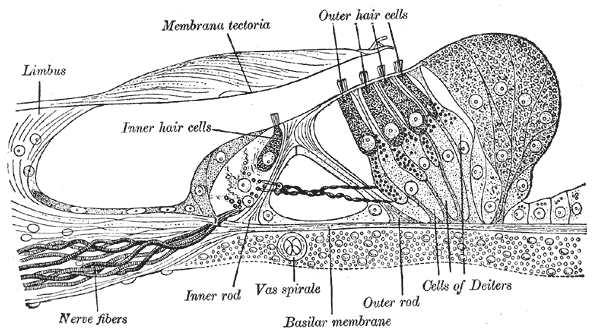
Fig. 71 Schéma de l’ogane de Corti. (Source : Gray’s Anatomy)

Chaque cellule ciliée interne est ainsi activée par les vibrations de la membrane basilaire à l’endroit précis où elle est fixée. Ceci permet de transmettre au nerf auditif l’information tonotopique évoquée précédemment, sous forme de signaux électriques : chaque fréquence sonore excite un groupe particulier de cellules ciliées, situé à une position spécifique le long de la cochlée – les fréquences élevées près de la base, les basses fréquences vers l’apex.

Mais ce n’est pas tout : l’onde sonore étant composée de fluctuations périodiques, les déplacements de la membrane basilaire et des stéréocils le sont également. La Fig. 72 représente la charge électrique d’une cellule en réponse à des tons purs de différentes fréquence. Pour des fluctuations relativement lentes (fréquences inférieures à 1 kHz), on observe effectivement que le potentiel électrique de la cellule suit assez fidèlement la périodicité de l’onde sonore. Ceci constitue le principe du codage temporel : les cellules ciliées s’activent de façon globalement synchrone avec les vibrations de la membrane basilaire. Il est donc possible de déduire la fréquence du son en observant la fréquence du signal électrique transmis.

Cependant, ce mécanisme de codage a ses limites. En effet, la cellule ciliée ne peut pas réagir instantanément à chaque mouvement des stéréocils : elle a besoin d’un temps très court pour se décharger avant de pouvoir être à nouveau activée. Pour des sons de fréquence basse, comme on l’a vu, ce délai est suffisamment court pour permettre à la cellule de suivre chaque cycle sonore. En revanche, lorsque la fréquence augmente au delà de 1 kHz, les fluctuations deviennent trop rapides pour que la cellule puisse réagir à chaque période de l’onde. Dans ce cas, la réponse électrique devient plus stable et plus constante. Au lieu de suivre les détails temporels fins du son, elle reflète alors surtout l’intensité moyenne de la fréquence considérée (Fig. 72).

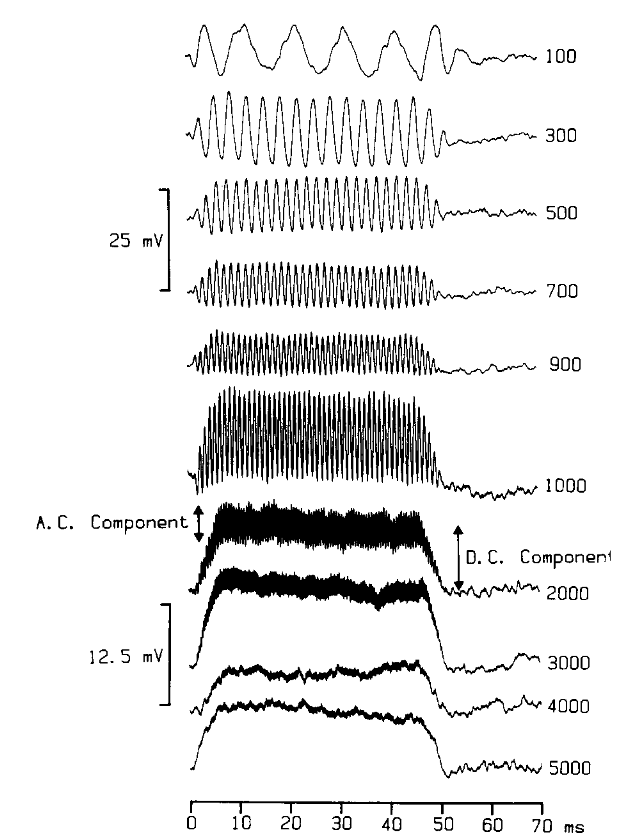
Fig. 72 Fluctuations du potentiel électrique de cellules cilliées en réponse à des tons purs à différentes fréquences. Pour des fréquences inférieures à 1 kHz, l’activité électrique présente une périodicité à la même fréquence que le son : c’est le codage temporel. Au dessus de 1 kHz, la cellule n’est plus en mesure de suivre les fluctuations rapides du son. (Palmer and Russel, 1986)

Le codage des fréquences par l’oreille interne est donc double. D’une part, chaque fréquence active une région spécifique de la membrane basilaire, mobilisant un sous-ensemble distinct de cellules ciliées (codage tonotopique). D’autre part, les fluctuations de la membrane basilaire suivent approximativement le rythme de l’onde, rendant le signal électrique lui-même périodique (codage temporel). Par ailleurs, ces deux codes présentent chacun des limitations spécifiques dans les hautes fréquences : le codage tonotopique devient de moins en moins précis pour les fréquences élevées, tandis que le codage temporel ne peut pas suivre fidèlement la périodicité du son au delà de 1 kHz environ.

Modéliser l’oreille interne (partie 2) : spectrogramme auditif

Nous avons vu précédemment comment le pattern d’excitation rend compte du codage tonotopique au sein de la cochlée. En revanche, cette représentation purement fréquentielle ne permet pas de visualiser le codage temporel, qui repose sur l’organisation dans le temps du signal. Pour explorer cette dimension, on peut toutefois examiner le décours temporel de la sortie de chaque filtre gammatone – qui modélise les oscillations de la membrane basilaire en un point spécifique. La figure suivante illustre ces vibrations en réponse à un complexe harmonique pour six gammatones de différentes fréquences d’accordage. Sans surprise, le gammatone centré sur la fréquence fondamentale (ici 300 Hz) produit un signal périodique à la méme fréquence. De même les gammatones à 600 Hz et à 1270 Hz sont fortement excités par les harmoniques à 600 Hz et à 1200 Hz, et leurs réponses font don apparaître des périodicités à 600 Hz et à 1200 Hz, respectivement. Ceci correspond au double code évoqué précédemment : non seulement la membrane basilaire est particulièrement excitée au point correspondant à la fréquence du son, mais ses oscillations suivent elles-mêmes cette fréquence. Nous reviendrons plus loin sur les fluctuations observées dans les réponses des gammatones situés dans les fréquences plus élevées (3460 Hz, 5060 Hz et 7350 Hz sur la Fig. 73).

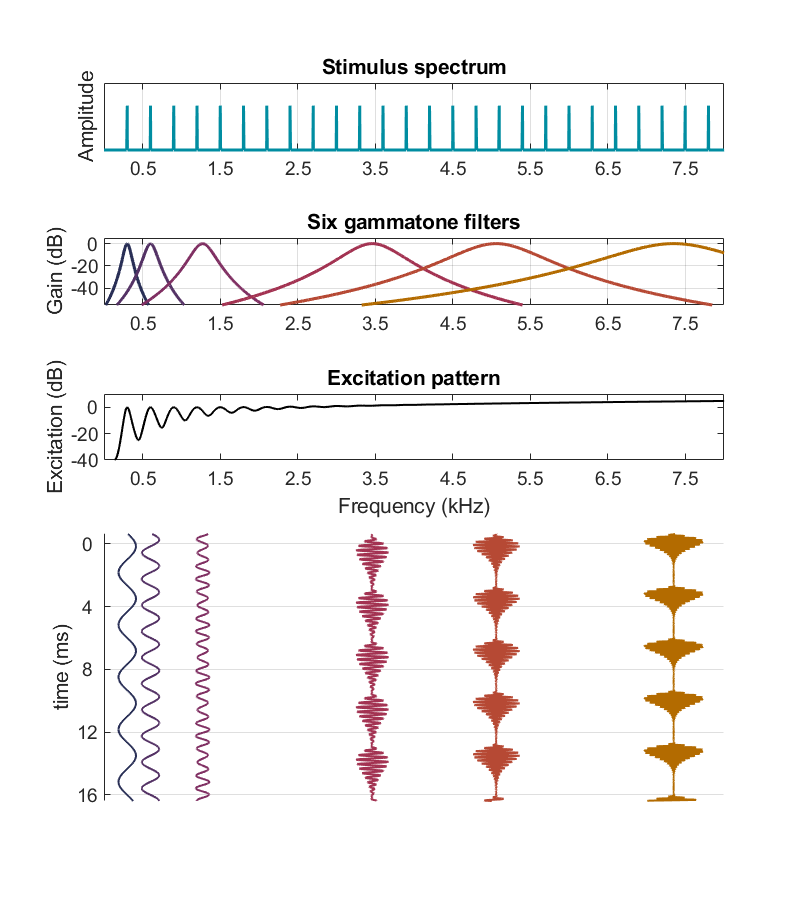
Fig. 73 Modélisation des vibrations en différents points de la membrane basilaire, en réponse à un complexe harmonique de fréquence fondamentalementale 300 Hz. Le spectre de ce signal est représenté dans le panneau supérieur. Comme pour la Fig. 65, on a tracé en-dessous les fonctions de transfert de six gammatones, de fréquences d’accordage 300 Hz, 600 Hz, 1270 Hz, 3460 Hz, 5060 Hz et 7350 Hz, puis le pattern d’excitation – qui fait bien apparaître les pics des harmoniques résolues dans les basses fréquences (300 Hz, 600 Hz, 900 Hz…). La partie inférieure de la figure présente la sortie temporelle de chacun des six gammatones identifiés plus haut. On observe une périodicité à 300 Hz dans la réponse du filtre gammatone accordé à 300 Hz, une périodicité à 600 Hz dans la réponse du filtre gammatone accordé à 600 Hz, et une périodicité à 1200 Hz dans la réponse du filtre gammatone accordé à 1270 Hz. (Inspiré de Plack, 2023)

Pour modéliser les fluctuations du potentiel électrique des cellules cilliées en réponse à un son, une approximation peut être obtenues en deux étapes simples : rectifier la sortie du gammatone en mettant à zéro les valeurs négatives (car les cellules ciliées se chargent lorsque les stéréocils sont pliés dans un sens, mais non dans l’autre), puis appliquer un filtrage passe-bas en dessous de 1 kHz (en effet, comme évoqué plus haut, les cellules ciliées sont incapables de suivre des fréquences au delà de 1 kHz environ). En affichant le résultat en fonction de la fréquence centrale du gammatone et du temps, on obtient une représentation spectro-temporelle appelée spectrogramme auditif (voir Fig. 74). Chaque ligne de cette représentation correspond à une fréquence d’accordage, c’est-à-dire une position le long de la cochlée, et les nuances de couleurs indiquent la charge electrique des cellules ciliées correspondantes au cours du temps.

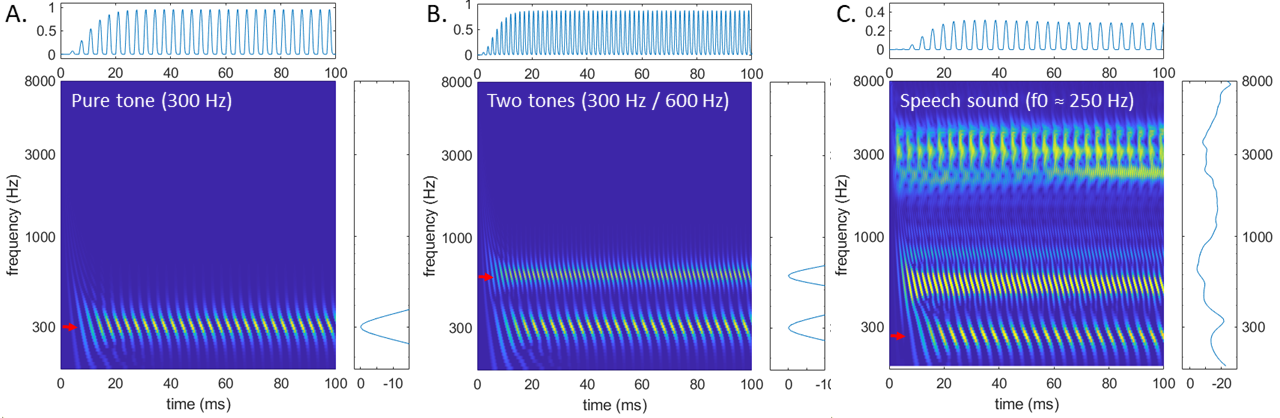
Fig. 74 Trois exemples de spectrogramme auditif, en réponse à un ton pur à 300 Hz (panneau A), à deux tons purs à 300 et 600 Hz (panneau B), et à un enregistrement de la voyelle “é” prononcée par une voix avec une fréquence fondamentalementale à 250 Hz (panneau C). A droite de chaque spectrogramme est représenté le pattern d’excitation correspondant, et au dessus la réponse électrique simulée d’une cellule ciliée particulière (c’est-à-dire une ligne du spectrogramme, identifiée par la flèche rouge) : cellule accordée à 300 Hz (panneau A), à 600 Hz (panneau B) ou à 250 Hz (panneau C).

Trois spectrogrammes auditifs sont représentés Fig. 74. Le premier correspond à l’écoute d’un simple ton pur à 300 Hz. On identifie aisément le codage tonotopique par la présence d’une bande horizontale, indiquant qu’une région de la cochlée est particulièrement excitée par le ton pur. Ce codage tonotopique se retrouve sur le pattern d’excitation (qui s’apparente à un spectrogramme auditif moyenné sur la dimension temporelle). Le spectrogramme auditif rend également compte du codage temporel, sous la forme d’une périodicité à 300 Hz de l’excitation 1]. Cette dernière est particulièrement bien visible lorsqu’on isole le taux de décharges simulé des cellules accordées à 300 Hz, qui reproduit assez fidèlement les observations de la Fig. 72. On retrouve ce double code tonotopique/temporel lorsqu’on considère le spectrogramme auditif de deux tons purs (Fig. 74B). Dans le cas du son de parole, on retrouve également les mêmes motifs tonotopiques et temporels. Sur la base de cette information, le cerveau peut donc “lire” la fréquence fondamentale du son (250 Hz) de plusieurs façons : en cherchant le premier pic d’excitation le long de l’axe des fréquences (aisément identifiable sur le pattern d’excitation), ou en analysant les périodicités temporelles dans cette représentation.

Cellules cilliées externes et amplification-compression

La troisième et dernière fonction de la cochlée est d’effectuer une compression de dynamique. En effet, l’oreille humaine est capable de percevoir des sons très faibles (de l’ordre de quelques dB SPL) mais également des sons très forts (le seuil de douleur se situant approximativement à 120 dB SPL). L’écart entre les deux représente une gamme d’environ 120 dB, c’est à dire un facteur 1 000 000 000 000 ! Ceci est rendu possible grâce à une étape d’amplification des signaux faibles lors de la transduction.

L’amplification est notamment assurée par les ~25000 cellules ciliées externes. Celles-ci sont disposées tout le long de la cochlée, comme les cellules ciliées internes, mais organisées en trois rangées (voir Fig. 71). Les deux types de cellules possèdent une structure similaire mais fonctionnent sur un principe opposé : tandis que les cellules ciliées internes convertissent un mouvement mécanique en impulsion électrique envoyée dans les fibres du nerf auditif, les cellules ciliées externes convertissent une impulsion électrique venue du nerf auditif en mouvement mécanique. Ainsi, la cellule ciliée externe se contracte sous l’effet d’une commande électrique, comme on le voit sur la vidéo suivante (Schnupp, Nelken & King, 2011). Cet enregistrement réalisé dans le laboratoire de J. Ashmore, montre une cellule ciliée externe isolée de cobaye, à laquelle une électrode a été fixée. Un signal électrique est envoyé, et la réponse motrice de la cellule est observée au microscope. Le son de la vidéo correspond au signal électrique : il s’agit d’un extrait de Rock Around the Clock de Bill Haley. La cellule se contracte au même tempo que le courant, et donc que la musique.

La cellule ciliée externe est donc capable de se contracter en réponse à une commande électrique. Étant fixée à la membrane basilaire et reliée par ses stéréocils à la membrane tectoriale, elle peut ainsi amplifier ou atténuer les oscillations au sein de la cochlée. Ce mécanisme actif de rétroaction peut être mis en évidence en comparant les tuning curves mesurées sur un organisme vivant et sur un organisme mort (voir figure suivante). Dans ce dernier cas le fonctionnement mécanique passif de la cochlée est toujours en œuvre, mais les mécanismes actifs – notamment liés aux cellules ciliées externes – sont éteints.

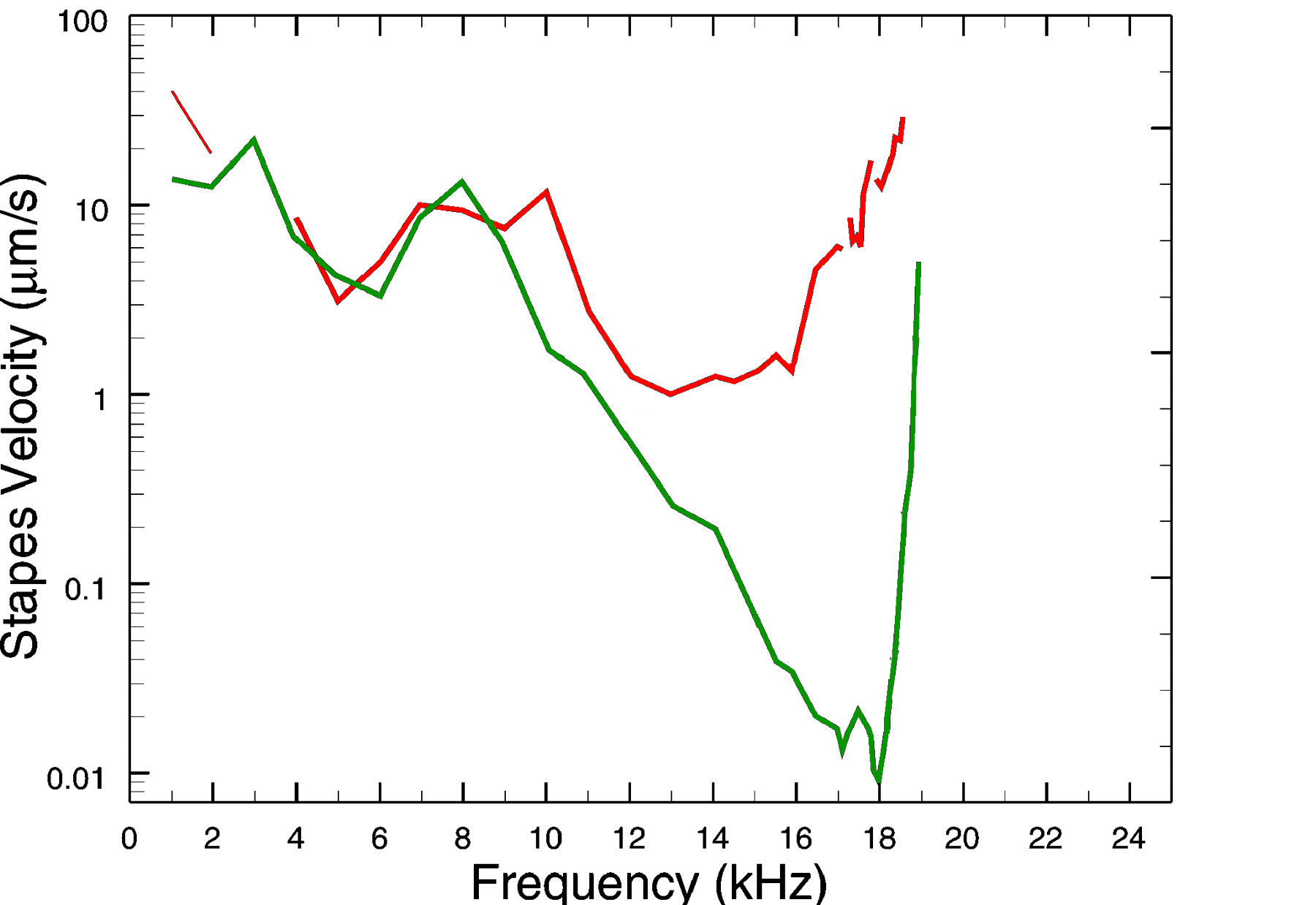
Fig. 75 Isoresponse tuning curves mesurée ante-mortem (courbe verte, similaire à la Fig. 62) ou post-mortem (courbe rouge, même mesure, mais sans action des mécanismes actifs). (Adapté de Nuttall & Dolan, 1996).

Comme on le constate sur la figure, la tuning curve mesurée post-mortem – et correspondant donc au fonctionnement purement mécanique de la cochlée – est très atténuée (facteur 100 par rapport à la tuning curve ante-mortem) et relativement larges. La viscosité de la périlymphe et la résistance de la membrane basilaire entraînent une grande déperdition d’énergie et on voit donc que l’idée d’une cochlée fonctionnant sur la seule base de l’énergie de l’onde entrante n’est pas tenable. Seule l’existence de mécanismes actifs compensant l’amortissement mécanique et améliorant la sélectivité fréquentielle permet d’expliquer la grande efficacité de la cochlée dans la transmission des signaux sonores de faible intensité.

Ce système de feedback actif est plus ou moins sollicité en fonction du niveau sonore : il renforce la perception des sons faibles mais laisse les sons forts être naturellement atténués. Ceci peut être observé en comparant les tuning curves mesurées en une même position pour des stimuli de différentes intensité (Fig. 76).

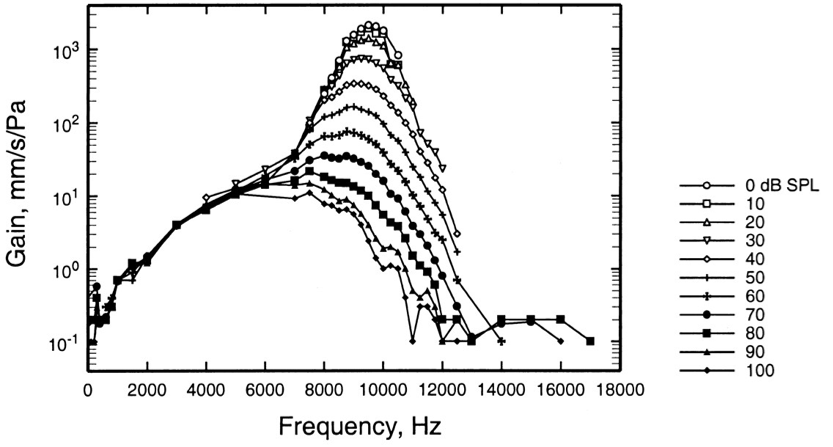
Fig. 76 Tuning curve pour une même cellule ciliée, mesurée avec différents volumes sonores pour la stimulation. Cette mesure met en évidence la non-linéarité du système : les sons faibles sont plus amplifiés que les sons forts, et la sélectivité est meilleure dans le premier cas. (Ruggero et al., 2000)

Lorsque le niveau sonore est faible, les tuning curves possédent une excellente résolution fréquencielle. En revanche, à des niveaux sonores élevés, la tuning curve devient très peu sélective et son gain maximum se trouve divisé par un facteur 100, indiquant que les vibrations sont fortement atténuées. De façon prévisible, le même phénomène peut également être observé au niveau des patterns d’excitation (voir Excitation.jpeg)

Modéliser l’oreille interne (partie 3) : DRNL

Il est possible d’améliorer notre modélisation précédente de la cochlée par un banc de filtres gammatones pour prendre en compte l’effet des cellules ciliées externes. Une première option très simple consiste à appliquer une fonction compressive (par exemple une loi puissance avec un exposant négatif) sur la sortie des gammatones. Ceci n’est cependant pas entièrement satisfaisant car la cochlée ainsi simulée, si elle réalise bien une compression de dynamique, conserve cependant la même résolution fréquencielle quel que soit le niveau sonore d’entrée. Une seconde option, légèrement plus sophistiquée, s’appuie sur des dual-resonance nonlinear filters (filtres DRNL). Ces filtres non-linéaires reproduisent l’évolution des tuning curves avec le niveau sonore, illustré Fig. 76. Leur réponse est calculée comme la somme des réponses de deux filtres passe-bande : le premier, linéaire et semblable aux gammatones mais avec une résolution plus faible, correspond à l’action mécanique du système, tandis que le deuxième, non-linéaire et plus sélectif en fréquence, rend compte des mécanismes actifs. La figure suivante illustre le gain d’un filtre DRNL accordé à 1000 Hz, lorsque le niveau sonore entrant est faible (30 dB SPL) ou fort (90 dB SPL). La réponse de la branche linéaire (en vert) est identique dans les deux cas ; en revanche la branche non-linéaire (en rouge) amplifie plus le son faible que le son fort. La somme des deux, en bleu, correspond à la sortie du DRNL et reproduit approximativement les observations de la Fig. 76.

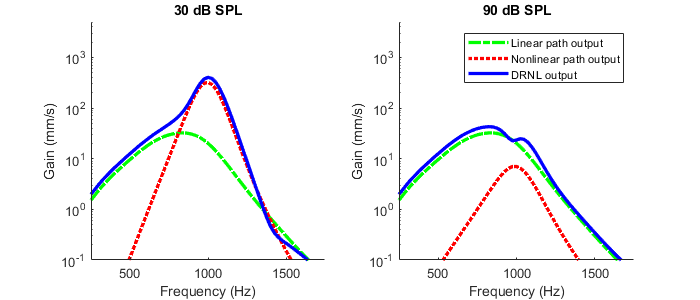
Fig. 77 Tuning curve simulée au moyen d’un filtre DRNL, pour un niveau sonore entrant de 30 dB SPL (gauche) ou de 90 dB SPL (droite). La courbe bleue correspond à la réponse en fréquence du DRNL, les courbes vertes et rouges à ses composantes linéaires et non-linéaires, respectivement. (inspiré de Lopez-Poveda & Meddis, 2001)

Une limite du modèle DRNL réside dans l’absence de prise en compte de la dynamique temporelle du contrôle de gain. Les filtres non linéaires décrits ci-dessus répondent de façon instantanée aux variations d’intensité du signal, ce qui constitue une simplification par rapport au fonctionnement du système auditif. En réalité, une certaine latence est nécessaire pour que le système détecte une variation du niveau sonore et transmette cette information aux cellules ciliées externes pour ajuster l’amplification. Cette propriété peut être intégrée dans le modèle en introduisant explicitement un délai, ou en modélisant la boucle de rétroaction. Néanmoins, ces aspects dynamiques sont souvent négligés en première approximation, afin de préserver la simplicité du modèle.

Nerf auditif

Comme nous l’avons mentionné plus haut, chaque cellule ciliée est connectée à un certain nombre de fibres du nerf auditif (environ une trentaine). Un différentiel électrique élevé à l’intérieur de la cellule se traduit généralement par le déclenchement d’un potentiel d’action dans les fibres. Les potentiels d’action étant toujours approximativement de même amplitude, c’est donc leur densité et leur organisation temporelle qui transmettent l’information sonore au cerveau. Ceci est illustré dans la Fig. 79 : la partie centrale de la figure schématise les trains d’impulsions électriques au sein de trois fibres du nerf auditif. Lorsqu’on considère en revanche la moyenne des impulsions sur un ensemble de fibres (partie inférieure de la figure), on retrouve un signal plus fin et continu.

Malgré ce système de transmission minimal, fait de séries d’impulsions électriques, le double codage des sons réalisé par la cochlée est maintenu au niveau du nerf auditif. D’une part, chaque fibre du nerf auditif étant connectée à une cellule ciliée particulière (elle même attachée à une région particulière de la membrane basilaire), elle est préférentiellement activée par certaines fréquences. Ce codage tonotopique se retrouve dans l’organisation des fibres au sein du nerf auditif : celles répondant préférentiellement aux fréquences aiguës se trouvent au centre et celles codant les fréquences graves en périphérie.

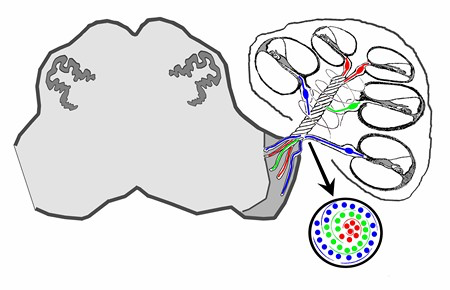
Fig. 78 Organisation tonotopique au sein du nerf auditif. Les fibres correspondant à trois gammes de fréquences, c’est-à-dire connectées à trois segments différents de la cochlée, sont identifiées en couleur : basse fréquence en rouge, fréquences médium en vert, hautes fréquences en bleu. (Source : P. Gil-Loyzaga).

D’autre part, le codage temporel observé dans la charge electrique des cellules ciliées est lui aussi maintenu au niveau du nerf auditif. En effet, les potentiels d’action suivent globalement l’activité électrique des cellules ciliés, et surviennent donc majoritairement aux pics du déplacement de la membrane basilaire – un phénomène nommé accrochage de phase (phase-locking). Les vibrations étant périodiques, les impulsions électriques envoyées au nerf auditif par les cellules ciliées présentent, elles aussi, une périodicité à la même fréquence. Comme illustré dans la Fig. 79 les décharges surviennennt globalement à proximité des maxima de la vibration, même si tous les maxima ne donnent pas nécessairement lieu à une décharge synchrone de toutes les cellules, certaines impulsions pouvant être absentes ou décalées. Néanmoins, chaque cellule émet des impulsions électriques avec une périodicité globalement alignée sur celle de l’onde. Dans la partie inférieure de la figure, la sommation des décharges transmises par l’ensemble des cellules ciliées au nerf auditif montre que, malgré une certaine variabilité, le signal global reproduit la périodicité du stimulus sonore.

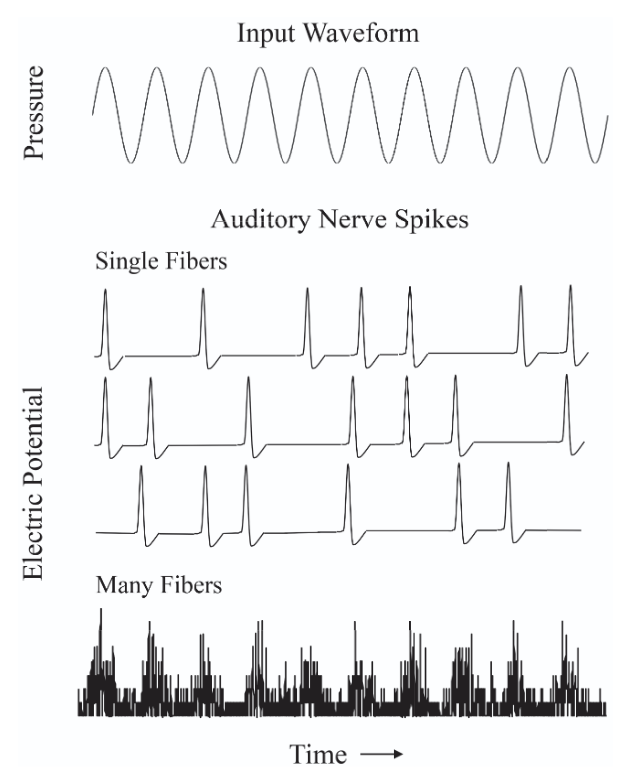
Fig. 79 Illustration du principe du codage temporel par accrochage de phase. La partie supérieure de la figure représente l’onde sonore. En dessous sont schématisés les potentiels évoqués générés par trois cellules ciliées internes accordées à la fréquence de cette onde, et transmis au nerf auditif. (Source: Plack 2018)

Il faut ici mentionner que le nerf auditif ne joue pas uniquement un rôle de transmetteur. Même si, considérées dans leur ensemble, les potentiels d’action semblent simplement véhiculer les codes tonotopique et temporel établis par la cochlée, en réalité la trentaine de fibres du nerf auditif connectées à une même cellule ciliée ne transmettent pas exactement la même information. Certaines fibres dites “à bas seuil” sont activés dès que la cellule ciliée correspondante est excitée, même légèrement, mais saturent ensuite rapidement (c’est à dire qu’elles ne distinguent pas une excitation moyenne d’une excitation forte). Au contraire, d’autres fibres dites “à haut seuil” ne se déclenchent qu’à partir d’un niveau relativement élevé d’excitation fe la cellule, tandis que les fibres “à moyen seuil” ont un comportement intermédiaire.

Certains modèles du système auditif périphérique permettent de simuler l’activité électrique au sein du nerf auditif. Pour cela, ils incluent, après le spectrogramme auditif, une étape simulant les réponses des différents types de fibres. Ce processus suit une loi aléatoire décidant du déclenchement ou non du potentiel d’action dans chaque fibre à un moment donné. La modélisation du nerf auditif n’est pas nécessaire pour les besoins de ce cours et cette étape du modèle ne sera donc pas considérée par la suite.

Références

Lopez-Poveda, E. A., & Meddis, R. (2001). A human nonlinear cochlear filterbank. The Journal of the Acoustical Society of America, 110(6), 3107–3118.

Nuttall, A. L., & Dolan, D. F. (1996). Steady‐state sinusoidal velocity responses of the basilar membrane in guinea pig. The Journal of the Acoustical Society of America, 99(3), 1556–1565.

Palmer, A. R., & Russell, I. J. (1986). Phase-locking in the cochlear nerve of the guinea-pig and its relation to the receptor potential of inner hair-cells. Hearing Research, 24(1), 1–15.

Plack, C. J. (2018). The Sense of Hearing (3rd edn). Routledge.

Ruggero, M. A., Narayan, S. S., Temchin, A. N., & Recio, A. (2000). Mechanical bases of frequency tuning and neural excitation at the base of the cochlea: Comparison of basilar-membrane vibrations and auditory-nerve-fiber responses in chinchilla. Proceedings of the National Academy of Sciences, 97(22), 11744–11750.

Schnupp, J., Nelken, I., & King, A. (2011). Auditory Neuroscience: Making Sense of Sound. MIT Press.

Notes

[5] On peut remarquer par ailleurs que la périodicité à 300 Hz semble formée de lignes diagonales descendantes. Il s’agit là d’un phénomène observé expérimentalement par von Bekésy et appelé “onde progressive” (traveling wave) : les ondes qui agitent la membrane basilaire ne sont pas stationnaires mais semblent progresser depuis la base vers l’apex.