Stimuli et dimension#
Le premier aspect à considérer lors de la mise en place d’une expérience de psychoacoustique est le choix des stimuli. Parmi les quatre caractéristiques décrites dans ce chapitre, le stimulus est sans nul doute la plus simple à déterminer puisqu’il découle directement de la question scientifique considérée. Néanmoins, il est important de s’arrêter sur les principes qui doivent guider le choix des stimuli. Ceci nous donnera également l’occasion de présenter très brièvement le cadre de la Théorie de la Détection du Signal.
Choix des stimuli et de la dimension d’intérêt#
En psychophysique, le choix des stimuli (et dans une certaine mesure de la tâche) doit être guidé par le principe de réductionnisme : les sons présentés aux sujets doivent être les plus simples possible de façon à solliciter uniquement le mécanisme cognitif étudié. Ainsi, par exemple, si je m’intéresse à la perception des sons du langage, mais non à l’intelligibilité des mots, je devrais utiliser des pseudo-mots sans signification, comme “balure”, “capoune”, ou “aga”, plutôt que des mots véritables, de façon à ne pas activer les mécanismes de l’accès au sens des mots – qui ne nous intéressent pas et risqueraient de perturber notre mesure. De même l’étude de la perception des fréquences doit se fonder en priorité sur des stimuli simples comme les tons purs ou les complexes harmoniques, plutôt que sûr des mélodies composées de multiples notes ayant chacune des durées particulières.
Cependant, le choix d’un type particulier de stimulus, comme le ton pur, n’est pas encore assez spécifique. En effet, les tons purs peuvent varier en fréquence, mais également en durée ou en intensité. Dans le cadre d’une expérience psychophysique, on se limitera donc à une (ou un petit nombre de) dimensions d’intérêt, c’est à dire de paramètres acoustiques dont on cherche à étudier l’effet sur la perception. On pourra ainsi utiliser des tons purs de différentes fréquence, mais de même durée et de même intensité. Ou encore des bruits de brouhaha formés par une superposition d’un nombre N de voix simultanées, mais dans une seule et même langue, avec des locuteur·ices parlant dans un même registre de voix, et sans présenter de vidéo de la situation en simultané.
De façon plus générale la construction des questions psychophysiques elles-mêmes est sous-tendue par une approche réductionniste. Il s’agit, comme on le verra dans les chapitres suivants, de réduire une question extrêment large (“comment perçoit-on les sons ?”) à des questions de plus en plus précises portant sur des mécanismes perceptifs de plus en plus spécifiques (“comment perçoit-on la hauteur tonale d’un son ?”, puis “comment perçoit-on la hauteur tonale d’une série harmonique ?”, puis “quel est le rôle de fréquence de la fondamentale dans la perception de la hauteur tonale d’une série harmonique ?”, etc.). En cela, la psychophysique ne se distingue pas de l’ensemble des sciences modernes, toutes construites en suivant un raisonnement réductionniste.
Un bref aperçu de la théorie de la détection du signal#
Une question qui se pose alors est de relier théoriquement la dimension d’intérêt des stimuli et la capacité d’un système à percevoir ces stimuli. Il s’agit d’une question centrale pour la théorie de la détection du signal, cadre mathématique dérivé de la théorie de l’information, et permettant de modéliser la capacité d’un système à séparer l’information du bruit. Cette théorie fut initialement développée pour les systèmes radar, mais rapidement appliqué à la perception humaine, notamment par David Green & John Swets.
Bien que [son développement] ait été motivé par des problèmes liés aux radars, la théorie de la détection du signal est une théorie généraliste. […] Cette généralité nous a conduit à penser qu’elle pourrait être également pertinente pour la détection d’un signal par un être humain. […] La théorie de la détection du signal offre un cadre d’analyse permettant une description réaliste du comportement de l’observateur·ice humain·e dans un grand nombre de tâches perceptuelles. (Green & Swets, Signal Detection Theory and Psychophysics, 1966)
Fonction psychométrique théorique#
Pour illustrer les objectifs et méthodes de la théorie de la détection du signal, considérons la situation suivante :
Nous sommes en possession d’un appareil permettant de mesurer l’énergie E d’un son. Au moyen de ce système nous analysons des stimuli de durée fixe composés soit d’un bruit seul (B) soit d’un bruit et d’un signal sonore cible (B+T). Nous souhaitons déterminer, sur la base de cette mesure d’énergie, si le signal sonore était présent ou non.
Pour simplifier le problème, nous supposons que le signal à détecter a une énergie mesurée de 1 (dans une unité arbitraire), notée d’, et que l’énergie du bruit suit une distribution gaussienne avec un écart-type de 1. On peut alors représenter la situation par la figure suivante:
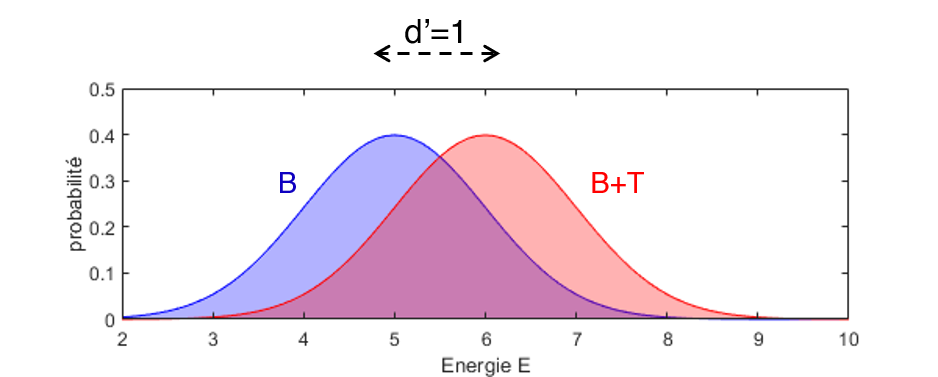
Fig. 6 Schéma de de la Théorie de la détection du signal. Les courbes rouge et bleue représentent respectivement les probabilités de mesurer une valeur particulière d’énergie E pour le bruit seul ou pour le bruit+signal#
Dans la situation décrite ci-dessus, il est possible, dans une certaine mesure, de détecter la présence ou l’absence du signal cible à partir de la valeur d’énergie E totale. Ainsi, pour une valeur de E = 7 on peut répondre de façon assez certaine que le signal cible était présent, tandis qu’une valeur E = 4 nous indique plutôt que le signal cible était absent. Pour des valeurs intermédiaires il est plus difficile de donner une réponse tranchée, mais une règle optimale dans ce cas serait de répondre “ton présent” pour toute valeur de E supérieure à 5.5, et ton absent sinon. Un calcul de probabilité permet de démontrer que l’application de cette règle dans la situation décrite précédemment produit 64% de réponses correctes en moyenne.
On peut à présent se demander comment ce pourcentage évolue en fonction de la difficulté de la tâche. Ici, le niveau de difficulté dépend directement de d’, la différence entre le son avec ou sans le signal. Cette distance entre les deux gaussienne jouera ici le rôle de dimension d’intérêt. À nouveau, il est possible de montrer par le calcul que la probabilité de détection en fonction de d’ suit une loi cumulative gaussienne, aussi appelée fonction logistique :
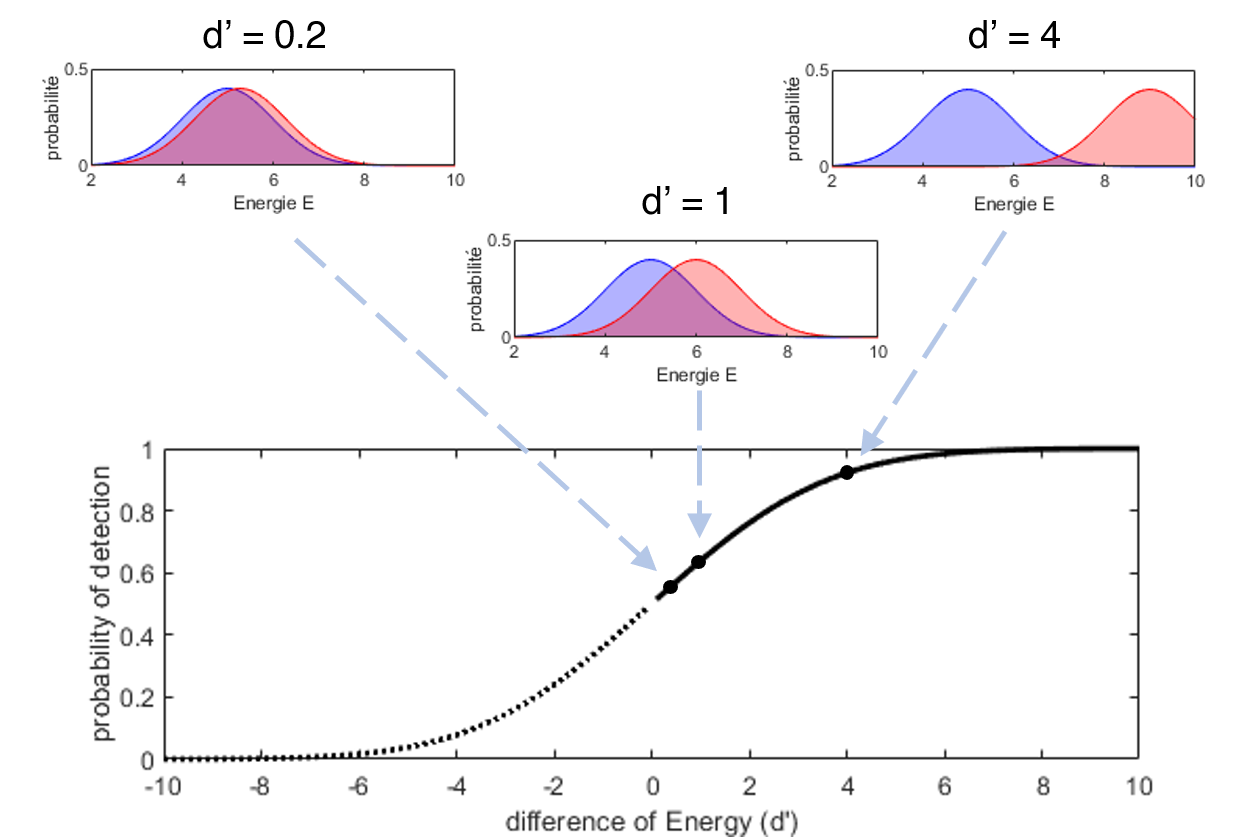
Fig. 7 Calcul de la fonction psychométrique pour la situation décrite précédemment#
Lorsque la distance entre les deux gaussiennes augmente, autrement dit lorsque les deux stimuli à différencier deviennent de plus en plus distincts, la tâche devient de plus en plus simple à réaliser. En effet, la fonction indique que le pourcentage de détections tend alors vers 100%. Au contraire lorsqu’on diminue l’énergie du ton jusqu’à d’ = 0 – un signal cible d’énergie nulle, autrement dit une tâche de détection impossible à réaliser – la probabilité chute à 50%, ce qui correspond au pourcentage de bonnes réponses obtenu en répondant au hasard. Cette fonction reliant la dimension d’intérêt au pourcentage de réponses est appelée fonction psychométrique et joue un rôle central dans la mesure en psychophysique comme on le verra dans la partie Méthode.
Notez que dans l’exemple choisi, d’ est toujours positif car il n’aurait pas de sens que l’énergie du signal+bruit soit moindre que celle du bruit seul. Néanmoins dans d’autres situations, il peut être pertinent de continuer la courbe auquel cas on obtient la fonction psychométrique complète, couvrant des probabilités de 0% à 100% (voir figure suivante).
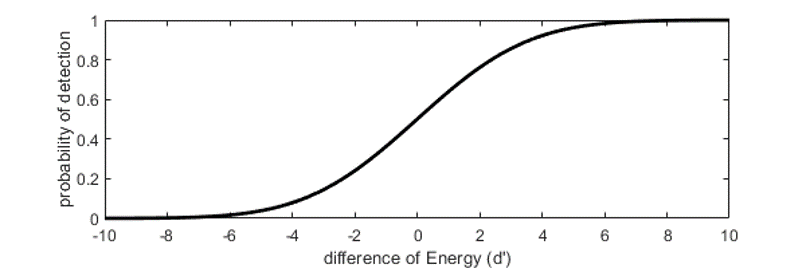
Fig. 8 Exemple de fonction psychométrique complète#
D’après l’équation ci-dessus, la forme de la fonction psychométrique est déterminée par deux paramètres, α et β [1].
α détermine le seuil à 50% de la fonction psychométrique, c’est à dire le niveau de la dimension d’intérêt à partir duquel on obtient plus de 50% de réponses correctes. Modifier ce paramètre revient donc à déplacer latéralement la fonction.
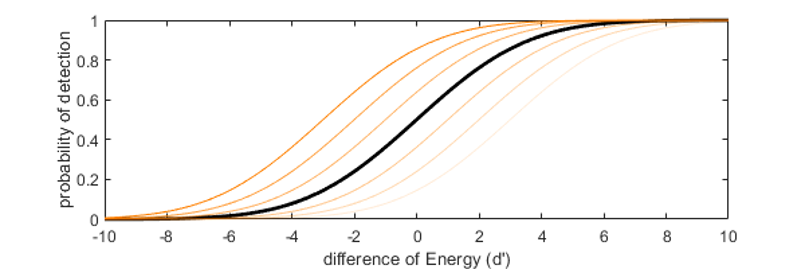
Fig. 9 Effet du paramètre alpha sur la fonction psychométrique.#
β détermine la pente de la fonction psychométrique, c’est à dire la sensibilité du système aux variations de la dimension d’intérêt. Pour de faibles valeurs de β, le pourcentage de réponses change peu lorsqu’on modifie la dimension d’intérêt (sensibilité faibles). Pour de fortes valeurs de pente en revanche, le pourcentage de réponses bascule brutalement de sa valeur minimum à sa valeur maximum dans un petit intervalle de la dimension d’inrêt (sensibilité élevé).
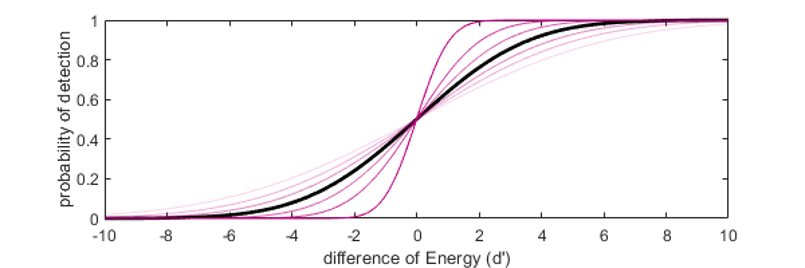
Fig. 10 Effet du paramètre beta sur la fonction psychométrique.#
Dans les paragraphes qui précèdent nous avons justifié théoriquement l’origine de la fonction psychométrique, pour l’exemple d’un détecteur électronique de signal sonore. Sachant que la fonction suit l’équation particulière décrite plus haut, nous pouvons caractériser empiriquement les performances de l’appareil en traçant sa fonction psychométrique ou, de façon équivalente, en indiquant son seuil à 50% et sa sensibilité, pour la dimension d’intérêt considérée. [2]
Fonction psychométrique humaine#
Ce cadre théorique s’applique non seulement aux appareils de détection comme celui décrit précédemment, mais également à l’humain, et se généralise à l’ensemble des expériences psychophysiques que nous allons rencontrer dans ce cours : pour des individus réalisant une tâche psychophysique, le pourcentage de réponses en fonction de la dimension d’intérêt suit (généralement) une fonction psychométrique logistique qu’il est possible de caractériser en termes de sensibilité et de seuil.
Voici par exemple les performances de sujets réalisant une tâche de détection de ton dans le bruit. Contrairement à l’exemple précédent, la dimension d’intérêt n’est pas la distance entre la gaussienne du bruit et celle du bruit + signal, mais le rapport signal sur bruit (RSB). Lorsque le RSB est élevé, la tâche est facile et les performances avoisinent donc les 100%. En revanche, lorsque le RSB tend vers -∞, les performances décroissent jusqu’au niveau du hasard, 50%. De même que dans le cas du détecteur électronique, on peut donc caractériser la perception humaine sur cette tâche en la décrivant par une valeur de seuil (on préférera ici le seuil à 75%) et une valeur de sensibilité. On utilise pour cela une régression logistique, procédure statistique qui permet d’ajuster une fonction logistique (la courbe continue) à un ensemble de données mesurées (les points) malgré la variabilité inhérente aux mesures empiriques chez l’humain. [3]
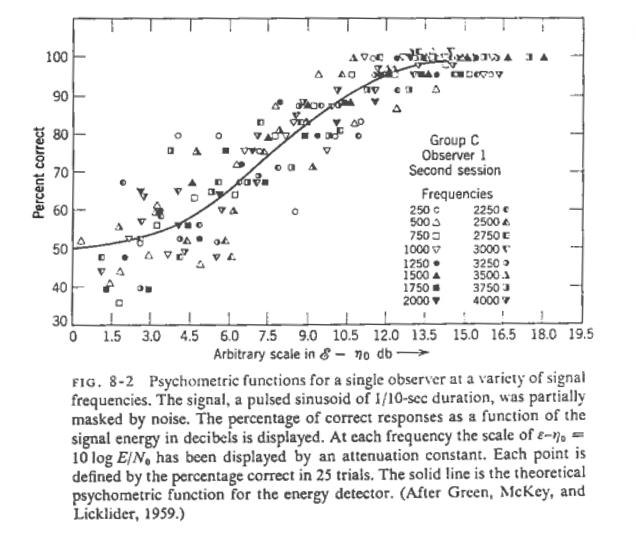
Fig. 11 Exemple de fonction psychométrique pour la détection de ton dans le bruit par l’humain. (Green & Swets, 1966).#
La figure suivante illustre un autre exemple d’application de la régression logistique, toujours dans le cadre d’une tâche de détection de ton dans le bruit avec le RSB comme dimension d’intérêt. Les différents symboles correspondent ici aux données collectées sur différents sujets. Une fonction psychométrique est ajustée individuellement pour chaque participant·e, puis caractérisée par son seuil à 80 %. Ce seuil, reporté sur l’axe des abscisses, sert ensuite de mesure simplifiée pour comparer les performances des participants. Ainsi, on constate ici que le sujet S5 se distingue par des performances nettement supérieures à celles de ses pairs, car le RSB auquel il·elle atteint 80 % de réponses correctes est nettement inférieur.
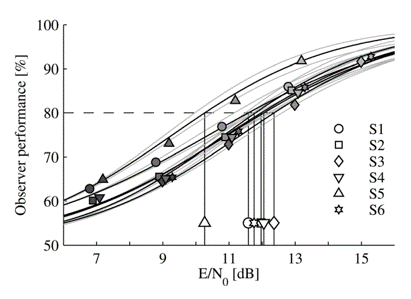
Fig. 12 Exemple de fonction psychométrique pour la détection de ton dans le bruit par l’humain. (Schönfelder & Wichmann, 2013).#
Finalement, la figure suivante présente un troisième exemple de fonction psychométrique humaine, cette fois pour une tâche de détection de ton pur dans le silence. En conséquence, la dimension d’intérêt n’est plus le RSB, mais l’énergie du signal en dB. Malgré l’absence de bruit de fond, on retrouve la forme sigmoïde caractéristique de la fonction psychométrique. La raison en est que le traitement sensoriel par le système auditif est lui-même bruité – par exemple, la transmission d’information dans les neurones est un processus partiellement aléatoire. On peut donc se ramener à la situation des deux gaussiennes décrites plus haut si l’on considère non plus le signal sonore parvenant au détecteur ou à l’oreille, mais l’influx nerveux conduisant à la décision “ton présent” ou “ton absent”.
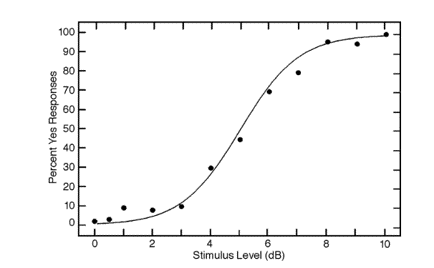
Fig. 13 Exemple de fonction psychométrique pour la détection de ton dans le silence par l’humain. (Leek, 2001).#
Au travers de la fonction psychométrique, la théorie de la détection du signal nous offre donc un cadre mathématique permettant relier le stimulus, et plus précisément sa dimension d’intérêt, à un pourcentage de réponses dans une tâche donnée. Elle répond donc parfaitement à l’objectif de la psychophysique qui est de relier monde physique et comportement observable. Dans la section suivante nous allons nous appuyer sur la fonction psychométrique pour décrire différentes méthodes expérimentales développées par les psychophysicien·nes.
Notes#
[1] De façon générale, on utilise généralement une équation incluant deux paramètres supplémentaires qui permettent de rentre compte des possibles erreurs d’inattention du sujet qui l’empêcheraient d’atteindre 100% de réponses correctes même dans le cas d’une tâche extrêmement simple, et du fait que le minimum de la fonction psychométrique peut être différent d’une expérience à l’autre.
[2] Il s’agit d’une présentation minimaliste de l’approche TDS. En réalité, une analyse complète devrait de plus distinguer deux types d’erreurs commises par le système : les Miss (le signal était présent mais n’a pas été détecté) et les False Alarms (détection du signal en son absence).
[3] En théorie, l’équation de la fonction psychométrique en fonction du RSB n’est pas la même que celle en fonction du d’. Néanmoins, en pratique, les chercheur·euses se limitent le plus souvent à l’équation de la loi logistique décrite plus haut.
Références#
Green, D. M., & Swets, J. A. (1966). Signal Detection Theory and Psychophysics. Peninsula Publishing.
Leek, M. R. (2001). Adaptive procedures in psychophysical research. Perception & Psychophysics, 63(8), 1279‑1292. https://doi.org/10.3758/BF03194543
Schönfelder, V. H., & Wichmann, F. A. (2013). Identification of stimulus cues in narrow-band tone-in-noise detection using sparse observer models. The Journal of the Acoustical Society of America, 134(1), 447‑463.
