Oreille interne, partie 1 : cochlée et membrane basilaire

L’oreille interne constitue le cœur du système auditif périphérique. Tandis que l’oreille externe et moyenne peut se réduire, en première approximation, à un simple filtre linéaire, l’oreille interne réalise plusieurs transformations essentielles des vibrations qui lui parviennent par la fenêtre ovale. Sa fonction est d’analyser les sons en fréquence, mais également d’amplifier les sons faibles et de convertir les vibrations mécaniques en signaux électriques.

L’oreille interne se décompose en trois parties :

• la cochlée, merveille de l’évolution qui, comme nous le verrons dans ce chapitre, est lui-même constitué de nombreux éléments en interaction.

• le nerf auditif, qui assure la jonction entre la cochlée et le système auditif central.

• le système vestibulaire. Ce dernier ne sera pas traité ici puisqu’il ne contribue pas à l’audition mais à l’équilibre.

Fig. 57 Schéma du système auditif périphérique mettant en évidence l’oreille interne. (Source : Ivy Livingstone, Biodidac)

Etant donnée la complexité de l’oreille interne, j’ai choisi de subdiviser sa description en deux chapitres. Cette première partie porte sur la membrane basilaire et son rôle dans la décomposition des sons en fréquences. Dans le chapitre suivant, nous explorerons le fonctionnement des cellules ciliées et du nerf auditif.

Cochlée, la membrane basilaire, et le codage tonotopique

La première fonction de la cochlée est de réaliser la décomposition de l’onde sonore en fréquence, c’est-à-dire de réaliser son analyse spectrale.

La cochlée possède une forme de coquille d’escargot – d’où son ancien nom français de “limaçon”, et sa racine latine cochlea. À l’intérieur, le conduit en spirale est divisé en deux sur presque toute sa longueur par une structure relativement rigide, la lame spirale, pour former deux canaux qui se rejoignent seulement au sommet (apex) et sont emplis d’un liquide appelé périlymphe [1]. Par ailleurs, la cochlée possède à sa base deux ouvertures couvertes d’une membrane : une entrée (la fenêtre ovale, attachée à l’étrier et donc reliée à l’oreille moyenne) et une sortie (la fenêtre ronde). L’onde communiquée par les mouvements de l’étrier au liquide contenu dans la cochlée peut donc suivre un trajet en double hélice, en remontant depuis la base de la cochlée jusqu’à son apex puis en redescendant pour ressortir par la fenêtre ronde. Ce cheminement du son est illustré sur la figure ci-dessous. Les canaux montant et descendant sont, rappelons-le, séparés par la lame spirale. Celle-ci possède une structure assez complexe à laquelle nous nous intéresserons plus loin. Dans l’immédiat, retenez que l’élément semi-rigide qui sépare le conduit montant du conduit descendant se nomme la membrane basilaire.

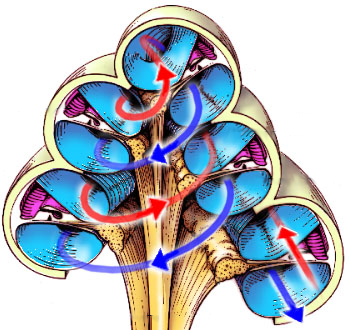
Fig. 58 Schéma de la cochlée et du chemin parcouru par l’onde sonore. Cette figure présente une vue en coupe transversale (Source : Neuroscience, Purves et al. 2019)

Dans son Traité de l’organe de l’ouïe, publié en 1683 et considéré comme le premier ouvrage d’otologie, Joseph-Guichard Du Verney décrit précisément la structure de la cochlée et propose sa première théorie fonctionnelle. Il remarque que la membrane basilaire n’est pas uniforme, mais varie en épaisseur et en résistance sur toute sa longueur : elle est étroite et rigide à la base, mais large et souple au niveau de l’apex. Du Verney émet donc l’hypothèse que ce gradient de propriétés physiques permet à la membrane basilaire d’être sensible à différentes fréquences en différents points.

[La membrane basilaire] n’est pas seulement capable de recevoir les tremblements de l’air, mais sa structure doit faire penser qu’elle peut répondre à tous leurs caractères différents. (Du Verney, Traité de l’organe de l’ouïe, 1683)

Fig. 59 Portraits de Joseph-Guichard Du Verney (1648-1730), Hermann von Helmholtz (1821-1894) et Georg von Békésy (1899–1972).

Hermann Von Helmholtz complètera cette théorie en 1863 en introduisant la notion de résonance – et en corrigeant quelques erreurs commises par Du Verney. L’idée est donc assez intuitive : lors de son trajet le long de la double hélice, l’onde sonore entraîne la membrane basilaire. Celle-ci ne vibre pas de façon uniforme ; au contraire du fait de son gradient de propriétés physiques, elle entre particulièrement en résonance en certains points correspondant aux fréquences contenues dans le son. La base est particulièrement sensible aux hautes fréquences (20 kHz) et l’apex aux basses fréquences (20 Hz). Ainsi, la cochlée réalise l’analyse spectrale des vibrations puisqu’une fréquence particulière excite une région particulière le long de la membrane basilaire. On appelle cette correspondance le codage de place ou codage tonotopique (c’est-à-dire “une fréquence = une position”).

Cette conception simple de la cochlée est suffisante pour la plupart des applications, et notamment pour les besoins de ce cours. Cependant, elle est partiellement erronée. C’est Georg von Békésy qui, sur la base d’une série d’expériences commencées en 1928, proposera l’approche moderne du fonctionnement de la cochlée, un travail qui lui valut de recevoir le prix Nobel de médecine en 1961. En effectuant des mesures précises de la membrane basilaire en mouvement, il démontre notamment que ses vibrations ne sont pas stationnaires comme on le supposait précédemment ; autrement dit celle-ci ne vibre pas comme une corde d’un instrument de musique. Les ondes sont au contraire transitoires, elles remontent le long de la membrane basilaire. De plus l’onde dans le liquide ne suit en réalité pas le trajet complet de la double hélice cochléaire. Le point de résonance de la membrane basilaire, d’impédance presque nulle, lui fournit un “raccourci” pour traverser la lame spirale et redescendre immédiatement sans passer par l’apex. Pour cette raison les vibrations de la membrane basilaire décroissent de façon très abrupte au delà du point de résonance. Les vidéos suivantes illustrent ce trajet pour des tons purs de fréquence aigue ou grave.

La figure ci-dessous illustre une mesure des vibrations de la membrane basilaire en réponse à un stimulus sonore, plus récente et plus précise que celle de von Békésy. Les scientifiques ont enregistré l’amplitude des vibrations de la membrane basilaire en différents points lorsqu’un ton pur à 15 kHz est diffusé. L’axe des abscisses représente la position le long de la membrane basilaire (plus proche de la base à gauche, plus proche de l’apex à droite), tandis que l’axe des ordonnées indique l’amplitude des vibrations mesurées. Conformément à nos attentes, les vibrations atteignent un maximum en un point particulier de la membrane – le point dont la résonance correspond à la fréquence du son – situé ici à environ 14,5 mm de l’apex. En termes de codage tonotopique, cette position spécifique “code” donc la fréquence de 15 kHz. Par ailleurs, l’excitation décroît rapidement au-delà de ce point (entre 14,5 mm et 13,5 mm), ce qui confère au profil général une asymétrie caractéristique, conformément aux observations pionnières de von Békésy.

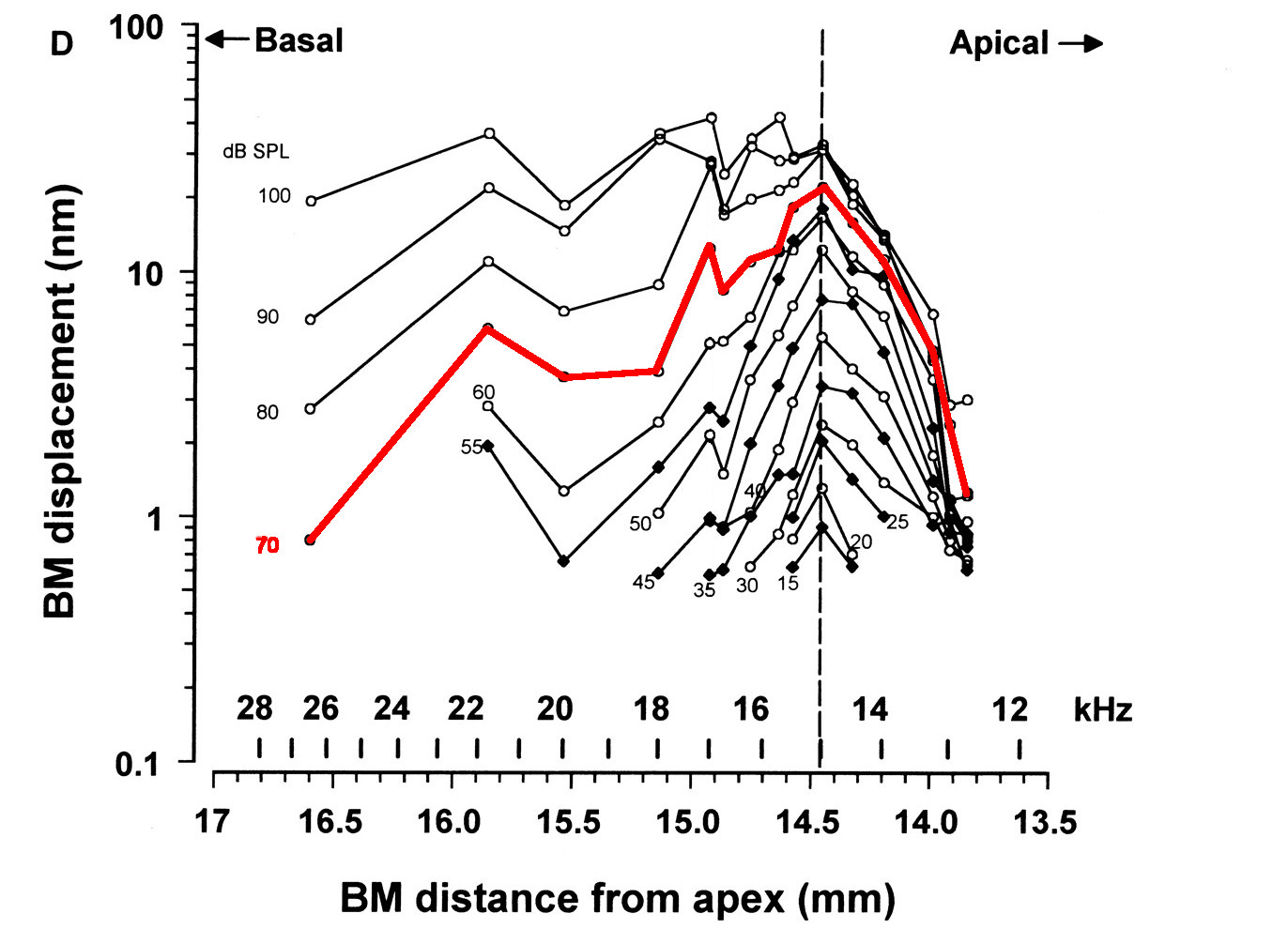
Fig. 60 Mesure de l’excitation de la membrane basilaire en réponse à un ton pur à 15 kHz, semblable à celles réalisées par von Békésy [2]. L’axe des abscisses correspond à la position considérée le long de la membrane – plus ou moins loin du sommet (apex) de la cochlée. L’axe des ordonnées représente l’amplitude des vibrations enregistrées en ce point. Plusieurs intensités du stimulus acoustique sont considérées, la courbe tracée en rouge correspondant à une intensité modérée de 70 dB SPL. (Russell and Nilsen, 1997 ; mesures obtenues chez le cobaye)

Pour être complet, un modèle mécanique de la cochlée doit intégrer un grand nombre de paramètres et d’équations de façon à simuler la mise en mouvement du liquide et la propagation de l’onde dans ce milieu, l’entraînement de la membrane basilaire – assimilée à une chaîne de resonnateurs couplés d’inertie mécanique variable – ainsi que les effets de rétroaction dont il sera question plus loin. Ce domaine fait donc actuellement l’objet d’importants travaux.

Mesure physiologique de la sélectivité fréquentielle de la cochlée

Comme on l’a vu, la cochlée réalise un codage tonotopique des sons, c’est-à-dire que chaque fréquence excite une région spécifique de la membrane basilaire. Toutefois, en tant que système mécanique soumis à l’inertie et au couplage entre régions voisines, elle ne peut effectuer qu’une analyse imparfaite des fréquences sonores. En particulier, sa résolution spectrale est limitée : deux tons purs de fréquences proches stimulent des zones similaires, et sont ainsi difficilement distinguables. L’organisation tonotopique de la cochlée et les limites de sa résolution peuvent être mises en évidence et quantifiées par des mesures physiologiques de l’excitation de la membrane basilaire en réponse à des tons purs. Nous avons déjà vu un exemple d’une telle approche à la Excitation.jpeg.

La figure suivante représente les tuning curves, une mesure de la sélectivité fréquentielle de la cochlée complémentaire de celle de la Excitation.jpeg. Chacune des courbes correspond à l’enregistrement des vibrations en une position unique le long de la cochlée, en fonction de la fréquence du ton pur joué (avec une intensité acoustique toujours identique).

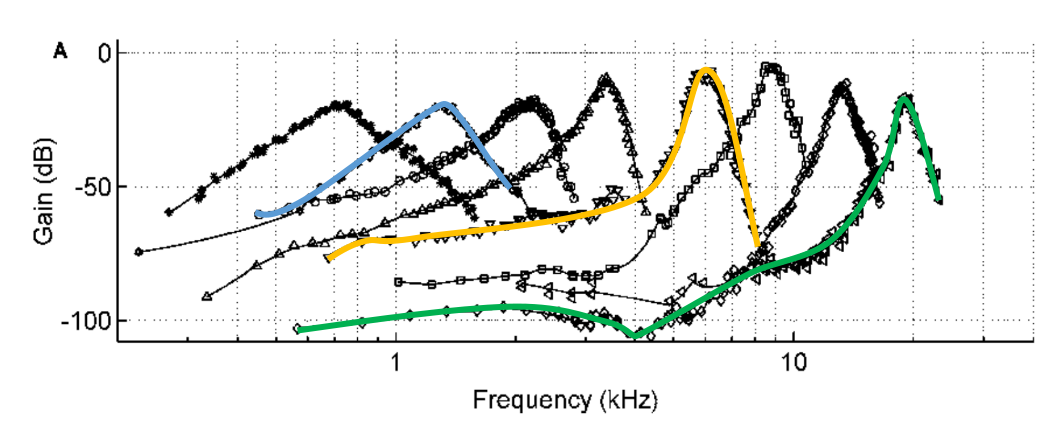
Fig. 61 Tuning curves. Chaque courbe représente la réponse de la membrane basilaire en un point particulier, en fonction de la fréquence du ton pur joué. Trois courbes sont mises en évidence, correspondant à l’enregistrement en trois positions specifiques. (Adapté de van der Heijden and Joris, 2003 ; mesures obtenues chez le chat)

Une approche expérimentale légèrement différente permet d’obtenir des courbes complémentaires, appelées isoresponse tuning curves. Plutôt que de mesurer la réponse de la membrane basilaire à intensité sonore constante, on ajuste ici le niveau de stimulation de manière à maintenir une réponse constante (c’est-à-dire une amplitude de vibration donnée de la membrane basilaire au point considéré). Comme on le constate dans la figure suivante, le tracé obtenu est globalement similaire à celui des tuning curves classiques (Fig. 61), mais inversé en raison de la nature de la mesure.

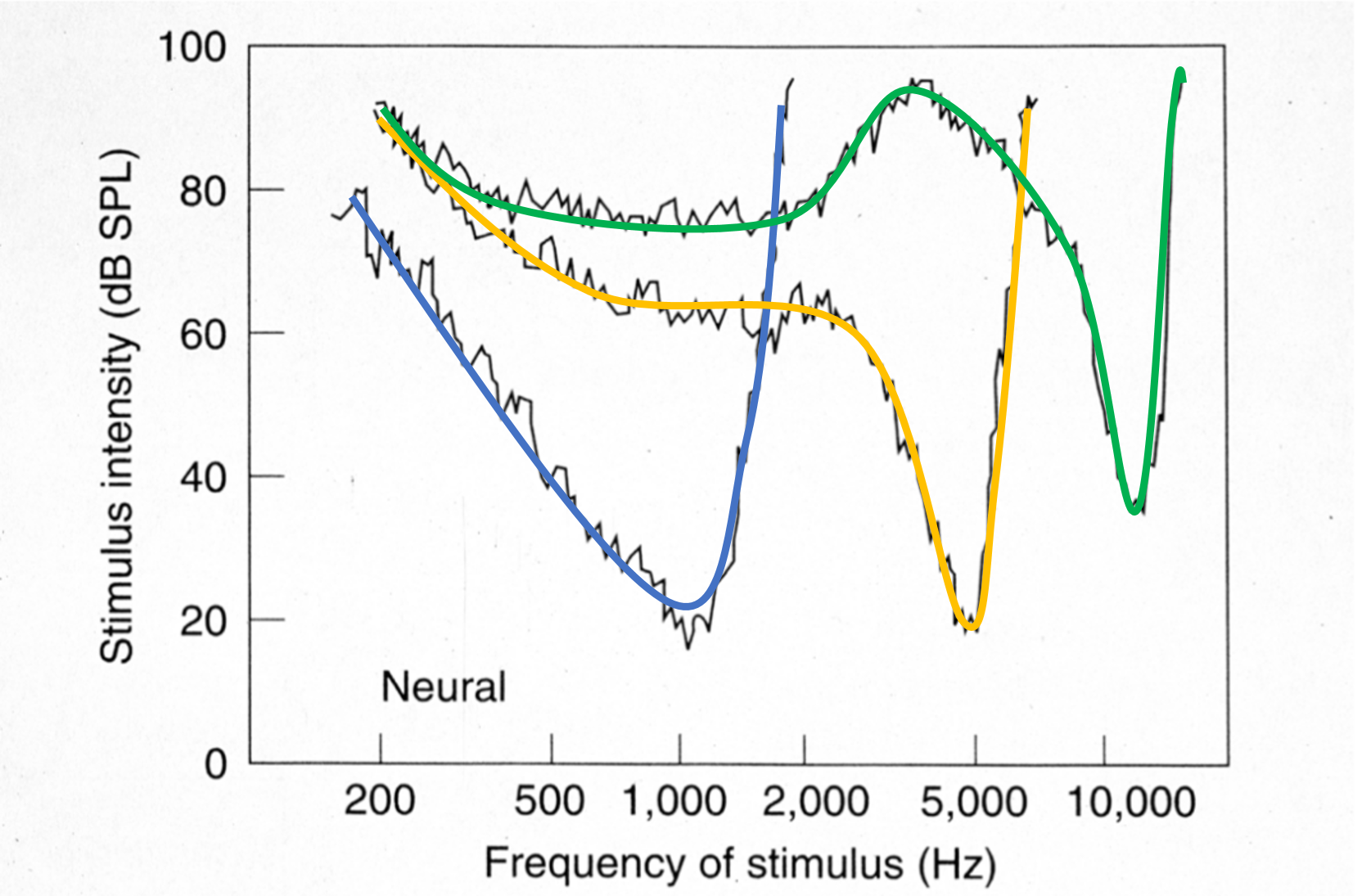
Fig. 62 Isoresponse tuning curves. Chaque courbe représente, en fonction de la fréquence du ton pur joué, l’intensité sonore nécessaire pour obtenir une excitation donnée de la membrane basilaire en un point particulier. Les tuning curves indiquées en couleurs correspondent approximativement à celles de la Fig. 61. (Kiang, 1980 ; mesures obtenues chez le chat).

Les observations dans les Excitation.jpeg, Fig. 61 et Fig. 62 confirment le codage tonotopique assuré par la cochlée : à chaque position le long de la membrane basilaire correspond une fréquence caractéristique (characteristic frequency), aussi appelée fréquence d’accordage (tuning frequency), pour laquelle l’excitation est maximale. Pour visualiser plus directement la correspondance entre position et fréquence, on peut reporter la fréquence d’accordage de chaque tuning curve en fonction de la distance à l’apex du point où a été réalisé la mesure, comme le montre la figure suivante.

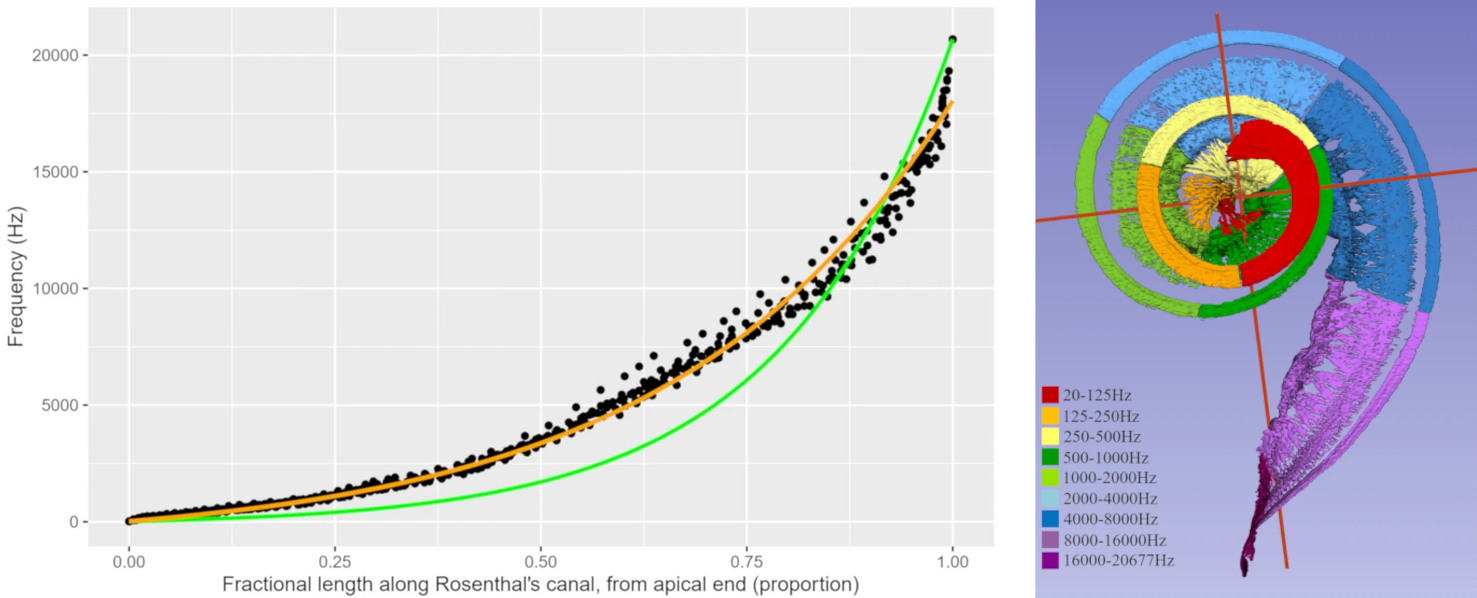
Fig. 63 À gauche : tonotopie de la cochlée, représentée par la fréquence caractéristique en fonction de la position relative le long de la membrane basilaire (0 : apex ; 1 : base). La courbe théorique couramment utilisée pour la modélisation est représentée en vert (équation de Greenwood), tandis que la courbe orange est ajustée aux données mesurée expérimentalement. Les positions les plus proches du sommet de la cochlée correspondent aux fréquences les plus basses. À droite : imagerie par rayons X d’une cochlée humaine, avec une visualisation en couleurs des zones correspondant aux différentes plages de fréquences. (Li, Helpard, Ekeroot, et al., 2021)

On observe que la relation entre fréquence d’accordage et distance à l’apex est globalement exponentielle. Il y a donc proportionnellement plus d’espace alloué aux basses fréquences qu’aux hautes fréquences, comme on le constate sur la partie droite de la Fig. 63. Dans les très basses fréquences (< 200 Hz), cette relation devient linéaire.

Les tuning curves révèlent non seulement la fréquence d’accordage d’une région donnée, mais aussi sa bande passante : une position donnée sur la membrane basilaire répond à un ensemble de fréquences proches, et non à une fréquence unique, ce qui reflète la limitation de la sélectivité fréquentielle de l’oreille interne. La largeur des courbes Fig. 61 et Fig. 62 constitue ainsi une mesure directe de cette sélectivité locale : plus la bande passante est étroite, plus la discrimination des fréquences est fine. Dans une première approximation nous considérerons que, pour l’humain, la largeur des tuning curves est proportionnelle à leur fréquence d’accordage (nous reviendrons sur ce point au chapitre 3). Autrement dit, les fréquences aiguës sont moins bien séparées par la cochlée que les fréquences graves. De façon générale, le facteur qualité Q (= largeur de bande / fréquence caractéristique) des tuning curves humaines est relativement mauvais, de l’ordre de 12%. Cette résolution assez faible de la cochlée suggère que d’autres mécanismes, plus haut niveau, entrent en jeu pour améliorer la précision de notre oreille.

Modéliser l’oreille interne : gammatones et pattern d’excitation

Sur la base de la description physiologique très sommaire de la cochlée que nous venons de donner, il est d’ores et déjà possible de mettre au point un modèle simpliste, mais pourtant efficace, de l’oreille interne. Ce modèle consiste exclusivement en une série de filtres linéaires, le banc de filtres gammatones. Chaque gammatone représente la fonction de transfert en une position spécifique le long de la membrane basilaire, c’est à dire une tuning curve particulière. Comme on l’a vu, la fréquence de résonance varie le long de la cochlée, de même que la résolution spectrale. Les filtres gammatones sont donc passe-bande de forme globalement triangulaire, avec une fréquence centrale et une largeur de bande variable. Ils sont espacés quasi-logarithmiquement entre 20 Hz et 20.000 Hz selon la fonction tonotopique vue plus haut (equation de Greenberg, fig xxx). Par ailleurs, ils ont un facteur qualité constant, c’est à dire que leur largeur de bande est proportionnelle à la fréquence centrale – ce qui est là encore cohérent avec les remarques faites plus haut sur la sélectivité fréquentielle des tuning curves [3]. La figure suivante illustre les fonctions de transfert d’un banc de gammatones.

Fig. 64 Fonction de transfert d’un banc de gammatones. Chaque courbe correspond à un gammatone individuel, c’est-à-dire à la fonction de transfert d’une position particulière le long de la membrane basilaire. Les trois gammatones indiqués en couleur sont ceux correspondant approximativement aux fréquences d’accordage à 1 kHz, 6 kHz et 11 kHz, mises en évidence dans les Fig. 61 et Fig. 63. La réponse des gammatones reprend grossièrement celle des tuning curves (Fig. 61; notez la différence d’échelle de fréquence entre les deux figures.)

Chaque gammatone permet donc de simuler l’excitation d’un point précis de la membrane basilaire en réponse à un son [4]. Pour obtenir un modèle de l’excitation tout au long de la membrane il suffit donc de calculer la réponse de chaque gammatone au son considéré. Le pattern d’excitation représente le niveau de sortie de chaque gammatone en fonction de sa fréquence d’accordage, offrant ainsi une simulation de l’excitation de la cochlée par un stimulus donné. La figure suivante illustre le calcul du pattern d’excitation en réponse à un ton pur de fréquence 1 kHz, à partir de la réponse de cinq gammatones.

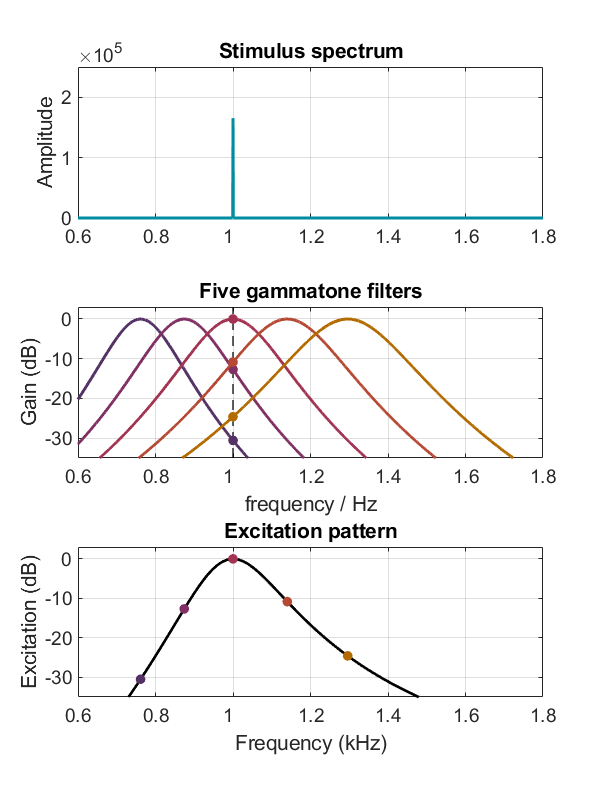
Fig. 65 Calcul du pattern d’excitation pour un ton pur de fréquence 1 kHz, dont le spectre de Fourier est représenté dans le panneau supérieur. Le panneau central présente les fonctions de transfert de cinq filtres gammatones particuliers, possédant des fréquences d’accordage de 762 Hz, 875 Hz, 1000 Hz, 1141 Hz et 1297 Hz. Pour chacun de ces gammatones, l’excitation par le ton pur à 1 kHz est indiquée par un point. Dans le panneau inférieur, ces cinq valeurs sont reportées en fonction de la fréquence d’accordage du gammatone. La courbe complète du pattern d’excitation est obtenue en reproduisant cette analyse pour toutes les fréquences d’accordage. (Figure inspirée de Moore & Glasberg, 1983)

La figure suivante représente le pattern d’excitation en réponse à un ton pur à 1.5 kHz. Cette simulation peut être rapprochée des valeurs d’excitation de la membrane basilaire représentées en Excitation.jpeg. Notez la différence d’échelle de fréquence entre les deux figures : l’axe des fréquences est inversé et les valeurs utilisées dans la simulation correspondent davantage à la gamme audible humaine.

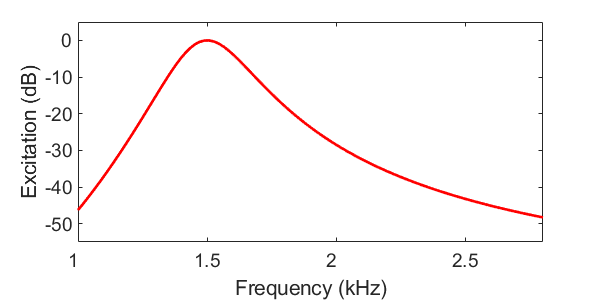
Fig. 66 Exemple de pattern d’excitation pour un ton pur à 1.5 kHz. Le pattern d’excitation reproduit deux caractéristiques majeures observées expérimentalement : la tonotopie (présence d’un maximum d’excitation) et l’asymétrie du pattern.

Comme nous le verrons par la suite le modèle du pattern d’excitation, bien qu’extrêmement simple, permet de rendre compte de nombreux phénomènes auditifs. Arrêtons nous sur quelques unes de ses propriétés. Tout d’abord, lorsque le stimulus est composé d’une fréquence unique, le pattern d’excitation possède quant à lui une certaine largeur de bande, reflétant la sélectivité limitée de l’oreille interne : un ton pur active non seulement le point de la membrane basilaire accordé sur cette fréquence mais également les régions adjacentes. Plus cette région est étendue moins la résolution spectrale est précise.

Autre caractéristique importante sur laquelle nous reviendrons, le pattern d’excitation d’un ton pur est asymétrique. En effet, les filtres gammatone situés au-dessus de la fréquence du stimulus étant plus larges que ceux situés en dessous, il en résulte un étalement de l’excitation vers les hautes fréquences, phénomène connu sous le nom d’upward spread of excitation.

Pour un complexe harmonique, composé de tons purs à des fréquences multiples d’une fréquence fondamentalementale, le pattern d’excitation fait apparaître une structure différente dans les basses et les hautes fréquences (voir figure ci-dessous). La résolution diminuant avec la fréquence, seules les premières harmoniques suscitent des pics d’excitation clairement séparés. On parle alors d’harmoniques résolues. Au contraire, dans les hautes fréquences, les harmoniques sont non-résolues : chaque gammatone couvrant plusieurs harmoniques il est impossible de distinguer ces dernières sur le pattern d’excitation. Nous reviendrons sur les implications auditives de ces propriétés du pattern d’excitation au chapitre 3.

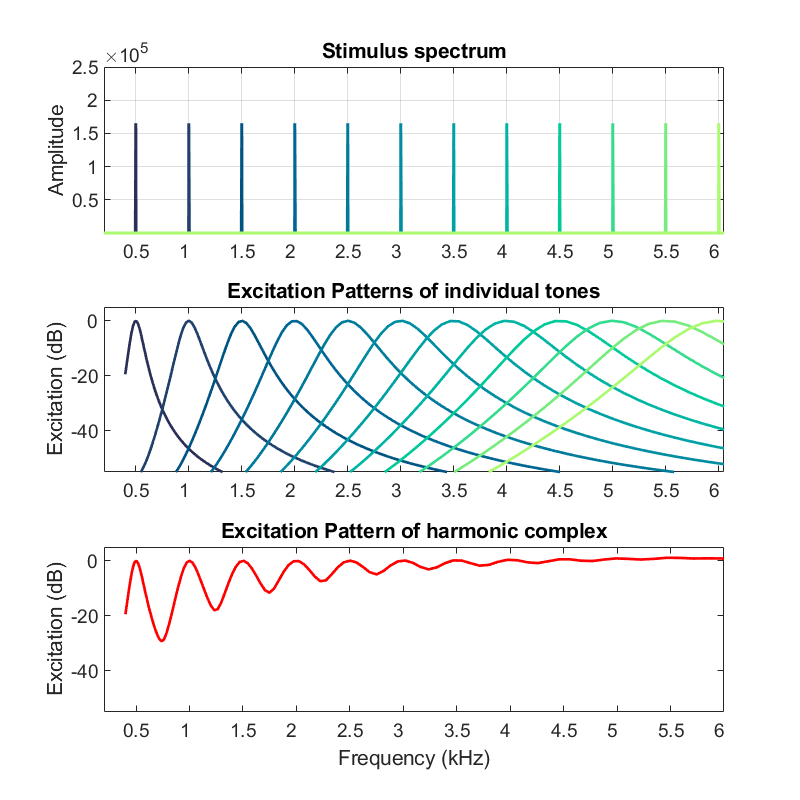
Fig. 67 Exemple de pattern d’excitation pour un complexe harmonique composé de tons purs à des multiples de 500 Hz, dont les spectres de Fourier sont représentés dans le panneau supérieur. Le panneau central présente le pattern d’excitation de chacun de ces tons purs, considérés individuellement, et le panneau inférieur le pattern d’excitation du compexe harmonique complet.

Avant d’explorer plus avant ce modèle, il est nécessaire d’envisager en premier lieu la dynamique temporelle du codage des sons par la cochlée. C’est ce à quoi nous allons nous atteler dans la section suivante.

Références

• Kiang, N.Y. (1980). Processing of speech by the auditory nervous system. J Acoust Soc Am. 1980 Sep;68(3):830-5.

• van der Heijden, M., Joris, P.X. (2003). Cochlear phase and amplitude retrieved from the auditory nerve at arbitrary frequencies. J Neurosci. 2003 Oct 8;23(27):9194-8.

• Russell, I.J., Nilsen K.E. (1997) The location of the cochlear amplifier: spatial representation of a single tone on the guinea pig basilar membrane. Proc Natl Acad Sci U S A. 1997 Mar 18;94(6):2660-4.

• Li, H., Helpard, L., Ekeroot, J. et al. (2021) Three-dimensional tonotopic mapping of the human cochlea based on synchrotron radiation phase-contrast imaging. Sci Rep 11, 4437.

• Moore, B. C., & Glasberg, B. R. (1983). Suggested formulae for calculating auditory-filter bandwidths and excitation patterns. The Journal of the Acoustical Society of America, 74(3), 750‑753. https://doi.org/10.1121/1.389861

Notes

[1] Notez qu’en réalité la cochlée est divisée non en deux mais en trois conduits, le troisième étant hermétiquement séparé des deux autres et empli d’un liquide différent, l’endolymphe. Ce détail n’est cependant pas important pour pour la présente description.

[2] Il s’agit ici de mesures effectuées chez le cochon d’Inde, d’où les fréquences testées particulièrement élevées, cette espèce possédant une gamme auditive plus étendue que celle de l’être humain. Mis à part cette différence, le système auditif périphérique des deux espèces demeure globalement comparable.

[3] La membrane basilaire étant continue il faudrait en théorie une infinité de gammatones pour la simuler complètement. Néanmoins, en pratique, on constate qu’un nombre relativement restreint de gammatones est suffisant pour la plupart des applications s’ils sont bien distribués selon la bonne loi de répartition en fréquence.

[4] Pour être complet, notre modèle simple du système périphérique devrait inclure les filtres d’oreille externe et moyenne suivis des filtres gammatones correspondant à l’oreille interne. Cependant, en pratique, les scientifiques utilisent le pattern d’excitation uniquement pour reproduire les phénomènes liés à la résolution de la membrane basilaire, et n’incluent donc pas de filtre d’oreille externe/moyenne.